7. Trigonometric Substitutions

On the previous page, we looked at tangent substitutions with coefficients. We now look a sine and secant substitutions with coefficients.

b2. Substitutions for \(a^2x^2-b^2\)

If the integrand involves the quantity \(b^2-a^2x^2\) (or \(a^2x^2-b^2\)) and you know that \(|x| \le \dfrac{b}{a}\), then it may be useful to make a substitution so that \(a^2x^2=b^2\sin^2\theta\). To do this, \(x=\dfrac{b}{a}\sin\theta\). (This is where you need \(|x| \le \dfrac{b}{a}\).) Then \(dx=\dfrac{b}{a}\cos\theta\,d\theta\) and:

\[\begin{aligned} b^2-a^2x^2 &=b^2-b^2\sin^2\theta=b^2(1-\sin^2\theta) \\ &=b^2\cos^2\theta \end{aligned}\] So it may be possible to re-express the integrand in terms of \(\sin\theta\) and \(\cos\theta\) only.

If the integrand involves the quantity \(a^2x^2-b^2\) (or \(b^2-a^2x^2\)) and you know that \(|x| \ge \dfrac{b}{a}\), then it may be useful to make a substitution so that \(a^2x^2=b^2\sec^2\theta\). To do this, \(x=\dfrac{b}{a}\sec\theta\). (This is where you need \(|x| \ge \dfrac{b}{a}\).) Then \(dx=\dfrac{b}{a}\sec\theta\tan\theta\,d\theta\) and:

\[\begin{aligned} a^2x^2-b^2 &=b^2\sec^2\theta-b^2=b^2(\sec^2\theta-1) \\ &=b^2\tan^2\theta \end{aligned}\] So it may be possible to re-express the integrand in terms of \(\tan\theta\) and \(\sec\theta\) only.

How do you know if \(|x| \le \dfrac{b}{a}\) or \(|x| \ge \dfrac{b}{a}\)?

You look at any quantities inside square roots such as \(\sqrt{b^2-a^2x^2}\) which needs a \(\sin\) substitution or \(\sqrt{a^2x^2-b^2}\) which needs a \(\sec\) substitution. If there is no square root, then you look at the limits on the integral, if any. Frequently, it is even easier to check whether \(\,x=0\,\) is an allowed value.
If it is, then use a \(\sin\) substitution.
If not, then use a \(\sec\) substitution.

Compute \(\displaystyle \int \dfrac{1}{\sqrt{4x^2-1}}\,dx\).

We need \(4x^2-1 \ge 0\) which means \(|x| \ge \dfrac{1}{2}\). So we substitute \(x=\dfrac{1}{2}\sec\theta\). Then \(dx=\dfrac{1}{2}\sec\theta\tan\theta\,d\theta\) and: \[\begin{aligned} \int \dfrac{1}{\sqrt{4x^2-1}}\,dx &=\int \dfrac{1}{\sqrt{\sec^2\theta-1}}\dfrac{1}{2}\sec\theta\tan\theta\,d\theta \\ &=\dfrac{1}{2}\int \dfrac{1}{\sqrt{\tan^2\theta}}\sec\theta\tan\theta\,d\theta =\dfrac{1}{2}\int \sec\theta\,d\theta \\ &=\dfrac{1}{2}\ln|\sec\theta+\tan\theta|+C \end{aligned}\] To substitute back, we already know that \(\sec\theta=2x\) from the definition of the substitution. We also need a formula for \(\tan\theta\) in terms of \(x\). We can find it from the Pythagorean identity \(\tan^2\theta=\sec^2\theta-1\). Then \[ \tan\theta=\sqrt{\sec^2\theta-1}=\sqrt{4x^2-1} \]

Or we can draw a right triangle with hypotenuse \(2x\) and adjacent side \(1\), so that \(\sec\theta=\dfrac{2x}{1}=2x\). Then the opposite side is \(\sqrt{4x^2-1}\) and \(\tan\theta=\dfrac{\sqrt{4x^2-1}}{1}=\sqrt{4x^2-1}\).

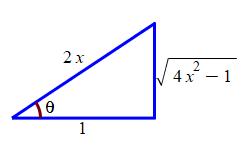
Returning to the problem at hand, we conclude: \[ \int \dfrac{1}{\sqrt{4x^2-1}}\,dx =\dfrac{1}{2}\ln\left|2x+\sqrt{4x^2-1}\right|+C \]

We check by differentiating. If \(f(x)=\dfrac{1}{2}\ln\left|2x+\sqrt{4x^2-1}\right|\), then \[\begin{aligned} f'(x) &=\dfrac{1}{2}\dfrac{1}{2x+\sqrt{4x^2-1}}\left(2+\dfrac{1}{2}\dfrac{8x}{\sqrt{4x^2-1}}\right) \\ &=\dfrac{1}{2x+\sqrt{4x^2-1}}\left(\dfrac{\sqrt{4x^2-1}+2x}{\sqrt{4x^2-1}}\right) =\dfrac{1}{\sqrt{4x^2-1}} \end{aligned}\] which is the integrand we started with.

Compute \(\displaystyle \int_0^2 \dfrac{1}{x^2-16}\,dx\).

From the limits, we know \(0 \le x \le 2\). So \(|x| \le 4\). So we substitute \(x=4\sin\theta\). Then \(dx=4\cos\theta\,d\theta\) and: \[\begin{aligned} \int_0^2 \dfrac{1}{x^2-16}\,dx &=\int_{x=0}^2 \dfrac{1}{16\sin^2\theta-16}4\cos\theta\,d\theta \\ &=\dfrac{1}{4}\int_{x=0}^2 \dfrac{\cos\theta}{-\cos^2\theta}\,d\theta =-\,\dfrac{1}{4}\int_{x=0}^2 \sec\theta\,d\theta \\ &=\left[-\,\dfrac{1}{4}\ln|\sec\theta+\tan\theta|\right]_{x=0}^2 \end{aligned}\]

To substitute back, we know \(\sin\theta=\dfrac{x}{4}\). So we draw a right triangle with opposite side \(x\) and hypotenuse \(4\), so that \(\sin\theta=\dfrac{x}{4}\). Then the adjacent side is \(\sqrt{16-x^2}\). Consequently, \[ \tan\theta=\dfrac{x}{\sqrt{16-x^2}} \quad \text{and} \quad \sec\theta=\dfrac{4}{\sqrt{16-x^2}} \]

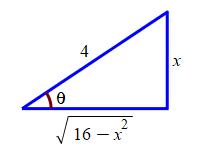
Returning to the problem at hand, we conclude: \[\begin{aligned} \int_0^2 \dfrac{1}{x^2-16}\,dx &=\left[-\,\dfrac{1}{4}\ln\left|\dfrac{4+x}{\sqrt{16-x^2}}\right|\right]_0^2 \\ &=-\,\dfrac{1}{4}\ln\dfrac{4+2}{\sqrt{16-2^2}}+\dfrac{1}{4}\ln\dfrac{4}{\sqrt{16}} \\ &=-\,\dfrac{1}{4}\ln(\sqrt{3}) \end{aligned}\]

When we see the expression \(x^2-16\), we normally think we should use a \(\sec\) substitution. However in this case, the limits on the integral say differently.

Compute \(\displaystyle \int \dfrac{1}{\sqrt{4-9x^2}}\,dx\)

Let \(3x=2\sin\theta\)

\(\displaystyle \int \dfrac{1}{\sqrt{4-9x^2}}\,dx =\dfrac{1}{3}\arcsin\dfrac{3x}{2}+C\)

Let \(9x^2=4\sin^2\theta\) or \(x=\dfrac{2}{3}\sin\theta\). Then \(dx=\dfrac{2}{3}\cos\theta\,d\theta\) and \[\begin{aligned} \int \dfrac{1}{\sqrt{4-9x^2}}\,dx &=\int \dfrac{1}{\sqrt{4-4\sin^2\theta}}\dfrac{2}{3}\cos\theta\,d\theta \\ &=\dfrac{1}{3}\int \dfrac{1}{\sqrt{\cos^2\theta}}\cos\theta\,d\theta =\dfrac{1}{3}\theta+C \\ &=\dfrac{1}{3}\arcsin\dfrac{3x}{2}+C \end{aligned}\]

We check by differentiating. If \(f(x)=\dfrac{1}{3}\arcsin\dfrac{3x}{2}\) then \[ f'(x) =\dfrac{1}{3}\dfrac{1}{ \sqrt{1-\dfrac{9x^2}{4}} }\dfrac{3}{2} =\dfrac{1}{\sqrt{4-9x^2}} \] which is the integrand we started with.

Compute \(\displaystyle \int \dfrac{1}{\sqrt{9x^2-4}}\,dx\)

Let \(3x=2\sec\theta\).

\(\displaystyle \int \dfrac{1}{\sqrt{9x^2-4}}\,dx =\dfrac{1}{3}\ln\left|\dfrac{3x}{2}+\dfrac{\sqrt{9x^2-4}}{2}\right|+C\)

Let \(9x^2=4\sec^2\theta\) or \(x=\dfrac{2}{3}\sec\theta\). Then \(dx=\dfrac{2}{3}\sec\theta\tan\theta\,d\theta\). So: \[\begin{aligned} \int \dfrac{1}{\sqrt{9x^2-4}}\,dx &=\int \dfrac{1}{\sqrt{4\sec^2\theta-4}}\dfrac{2}{3}\sec\theta\tan\theta\,d\theta \\ &=\dfrac{1}{3}\int \dfrac{\sec\theta\tan\theta}{\sqrt{\sec^2\theta-1}}\,d\theta =\dfrac{1}{3}\int \dfrac{\sec\theta\tan\theta}{\sqrt{\tan^2\theta}}\,d\theta \\ &=\dfrac{1}{3}\int \sec\theta\,d\theta =\dfrac{1}{3}\ln|\sec\theta+\tan\theta|+C \end{aligned}\]

To substitute back, we know \(\sec\theta=\dfrac{3x}{2}\). So: \[\begin{aligned} \tan\theta&=\sqrt{\sec^2\theta-1} =\sqrt{\dfrac{9x^2}{4}-1} \\ &=\dfrac{\sqrt{9x^2-4}}{2} \end{aligned}\] Or we can look at the triangle and conclude \(\tan\theta=\dfrac{\sqrt{9x^2-4}}{2}\).

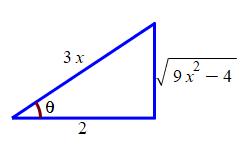
Then: \[\begin{aligned} \int \dfrac{1}{\sqrt{9x^2-4}}\,dx &=\dfrac{1}{3}\ln\left|\dfrac{3x}{2}+\dfrac{\sqrt{9x^2-4}}{2}\right|+C \\ &=\dfrac{1}{3}\ln\left|3x+\sqrt{9x^2-4}\right|-\dfrac{1}{3}\ln 2+C \end{aligned}\]

We check by differentiating. If \(f(x)=\dfrac{1}{3}\ln\left|3x+\sqrt{9x^2-4}\right|\), then \[\begin{aligned} f'(x) &=\dfrac{1}{3}\dfrac{1}{3x+\sqrt{9x^2-4}} \left(3+\dfrac{9x}{\sqrt{9x^2-4}}\right) \\ &=\dfrac{1}{3x+\sqrt{9x^2-4}}\left(\dfrac{\sqrt{9x^2-4}+3x}{\sqrt{9x^2-4}}\right) =\dfrac{1}{\sqrt{9x^2-4}} \end{aligned}\] which is the integrand we started with.

For each of the following integrals, choose which substitution to make.

\(x=\dfrac{4}{3}\sin\theta\) \(x=\dfrac{4}{3}\sec\theta\) \(x=\dfrac{3}{4}\sin\theta\) \(x=\dfrac{3}{4}\sec\theta\)

\(\displaystyle \int_{1/4}^{1/3} \dfrac{1}{16-9x^2}\,dx\)

A. Correct
To get the coefficients to match, we need \(x=\dfrac{4}{3}\sin\theta\) or \(x=\dfrac{4}{3}\sec\theta\).
Since \(\dfrac{1}{4} \le x \le \dfrac{1}{3}\), we have \(x \lt \dfrac{4}{3}\). So \(x=\dfrac{4}{3}\sin\theta\).

B. Incorrect
Look at the limits.

C. Incorrect
To get the coefficients to match, we need \(9x^2=16\sin^2\theta\) or \(9x^2=16\sec^2\theta\).

D. Incorrect
To get the coefficients to match, we need \(9x^2=16\sin^2\theta\) or \(9x^2=16\sec^2\theta\).
Also, look at the limits.
\(\displaystyle \int_{1/4}^{1/3} \dfrac{1}{16x^2-9}\,dx\)

A. Incorrect
To get the coefficients to match, we need \(16x^2=9\sin^2\theta\) or \(16x^2=9\sec^2\theta\).

B. Incorrect
To get the coefficients to match, we need \(16x^2=9\sin^2\theta\) or \(16x^2=9\sec^2\theta\).
Also, look at the limits.

C. Correct
To get the coefficients to match, we need \(x=\dfrac{3}{4}\sin\theta\) or \(x=\dfrac{3}{4}\sec\theta\).
Since \(\dfrac{1}{4} \le x \le \dfrac{1}{3}\), we have \(x \lt \dfrac{3}{4}\). So \(x=\dfrac{3}{4}\sin\theta\).

D. Incorrect
Look at the limits.
\(\displaystyle \int_{3}^4 \dfrac{1}{9-16x^2}\,dx\)

A. Incorrect
To get the coefficients to match, we need \(16x^2=9\sin^2\theta\) or \(16x^2=9\sec^2\theta\).
Also, look at the limits.

B. Incorrect
To get the coefficients to match, we need \(16x^2=9\sin^2\theta\) or \(16x^2=9\sec^2\theta\).

C. Incorrect
Look at the limits.

D. Correct
To get the coefficients to match, we need \(x=\dfrac{3}{4}\sin\theta\) or \(x=\dfrac{3}{4}\sec\theta\).
Since \(3 \le x \le 4\), we have \(x \gt \dfrac{3}{4}\). So \(x=\dfrac{3}{4}\sec\theta\).
\(\displaystyle \int_{3}^4 \dfrac{1}{9x^2-16}\,dx\)

A. Incorrect
Look at the limits.

B. Correct
To get the coefficients to match, we need \(x=\dfrac{4}{3}\sin\theta\) or \(x=\dfrac{4}{3}\sec\theta\).
Since \(3 \le x \le 4\), we have \(x \gt \dfrac{4}{3}\). So \(x=\dfrac{4}{3}\sec\theta\).

C. Incorrect
To get the coefficients to match, we need \(9x^2=16\sin^2\theta\) or \(9x^2=16\sec^2\theta\).
Also, look at the limits.

D. Incorrect
To get the coefficients to match, we need \(9x^2=16\sin^2\theta\) or \(9x^2=16\sec^2\theta\).

7. Trigonometric Substitutions

b2. Substitutions for \(a^2x^2-b^2\)

How do you know if \(|x| \le \dfrac{b}{a}\) or \(|x| \ge \dfrac{b}{a}\)?

Heading